Contents

Ejercicio 2

Hallar el vector X para la siguiente ecuación matricial:

A=[4 -2 -10;2 10 -12;-4 -6 16];
b=[-10 32 -16]';
x=A\b

x =

    2.0000
    4.0000
    1.0000

Ejercicio 4

A=[0 1 -1;-6 -11 6;-6 -11 5];

[P,D]=eig(A) % P autovectores, D autovalores
% Comprobacion de que el resultado es correcto
M1=A*P
M2=P*D

P =

    0.7071   -0.2182   -0.0921
    0.0000   -0.4364   -0.5523
    0.7071   -0.8729   -0.8285


D =

   -1.0000         0         0
         0   -2.0000         0
         0         0   -3.0000


M1 =

   -0.7071    0.4364    0.2762
   -0.0000    0.8729    1.6570
   -0.7071    1.7457    2.4856


M2 =

   -0.7071    0.4364    0.2762
   -0.0000    0.8729    1.6570
   -0.7071    1.7457    2.4856

Ejercicio 5

Determinar los voltajes de los nodos V1 y V2 y la potencia entregada por cada fuente:

Y=[1.5-2i -0.35+1.2i;-0.35+1.2i 0.9+1.6i];
I=[30+40i;20+15i];
V=Y\I;
% Voltajes en los nodos:
V1=V(1)
V2=V(2)
C=conj(I);
% Potencia entregada por las fuentes:
S=V.*C

V1 =

   0.6452 +10.9622i


V2 =

  17.4904 -11.0245i


S =

   1.0e+02 *

   4.5785 + 3.0306i
   1.8444 - 4.8285i

Ejercicio 6

Función recursiva problema de la Torres de Hanoi para un valor de 5 discos:

hanoi(5,'A','B','C')

Mover disco 1 de A a C
Mover disco 2 de A a B
Mover disco 1 de C a B
Mover disco 3 de A a C
Mover disco 1 de B a A
Mover disco 2 de B a C
Mover disco 1 de A a C
Mover disco 4 de A a B
Mover disco 1 de C a B
Mover disco 2 de C a A
Mover disco 1 de B a A
Mover disco 3 de C a B
Mover disco 1 de A a C
Mover disco 2 de A a B
Mover disco 1 de C a B
Mover disco 5 de A a C
Mover disco 1 de B a A
Mover disco 2 de B a C
Mover disco 1 de A a C
Mover disco 3 de B a A
Mover disco 1 de C a B
Mover disco 2 de C a A
Mover disco 1 de B a A
Mover disco 4 de B a C
Mover disco 1 de A a C
Mover disco 2 de A a B
Mover disco 1 de C a B
Mover disco 3 de A a C
Mover disco 1 de B a A
Mover disco 2 de B a C
Mover disco 1 de A a C

Ejercicio 7

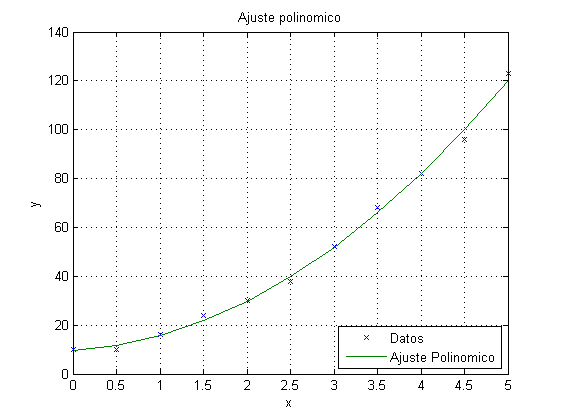
Ajustar un polinomio de orden 2 a los siguientes datos y graficar los puntos dados con el símbolo x y la curva ajustada con una línea sólida. Colocar una leyenda adecuada, etiquetas en los ejes y un título al gráfico.

x=0:0.5:5;
y=[10 10 16 24 30 38 52 68 82 96 123];
p=polyfit(x,y,2);
yc=polyval(p,x)
plot(x,y,'x',x,yc)
xlabel('x'),ylabel('y'),grid,title('Ajuste polinomico')
legend('Datos','Ajuste Polinomico',4)

yc =

  Columns 1 through 7

    9.6783   11.6895   15.7124   21.7469   29.7930   39.8508   51.9203

  Columns 8 through 11

   66.0014   82.0942  100.1986  120.3147

Ejercicio 8

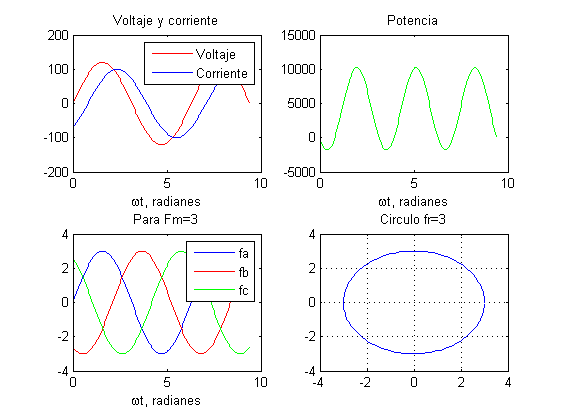
%Partir la ventana Figure en cuatro particiones (2x2) y graficar las siguientes funciones
%para wt de 0 a 3p en pasos de 0.05
%* Graficar v = 120 seno wt e i = 100 seno(wt - p/4 ) en función de wt en la parte superior izquierda
%* Graficar p = vi en la parte superior izquierda
%* Para Fm = 3.0, graficar fa = Fm seno wt, fb = Fm seno(wt – 2 p/3) y fc = Fm seno(wt – 4 p/3) en función de wt en la parte inferior izquierda
%* Para fR = 3.0, construir un círculo de radio fR en la parte inferior derecha

wt=0:0.05:3*pi;
v=120*sin(wt);
i=100*sin(wt-pi/4);
subplot(2,2,1), plot(wt,v,'r',wt,i),title('Voltaje y corriente'),legend('Voltaje','Corriente'),xlabel('\omegat, radianes')
p=v.*i;
subplot(2,2,2), plot(wt,p,'g'),title('Potencia'),xlabel('\omegat, radianes')
Fm=3;
fa=Fm*sin(wt);
fb=Fm*sin(wt-2*pi/3);
fc=Fm*sin(wt-4*pi/3);
subplot(2,2,3), plot(wt,fa,wt,fb,'r',wt,fc,'g'),title('Para Fm=3'),legend('fa','fb','fc'),xlabel('\omegat, radianes')
fr=3;
fi=0:0.05:2*pi;
x=fr*cos(fi);
y=fr*sin(fi);
subplot(2,2,4), plot(x,y);title('Circulo fr=3'),grid on

Ejercicio 13

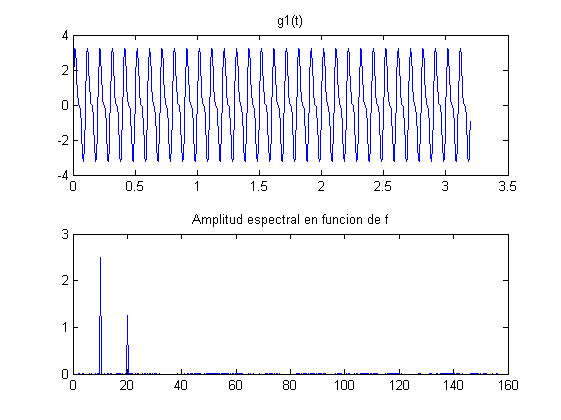
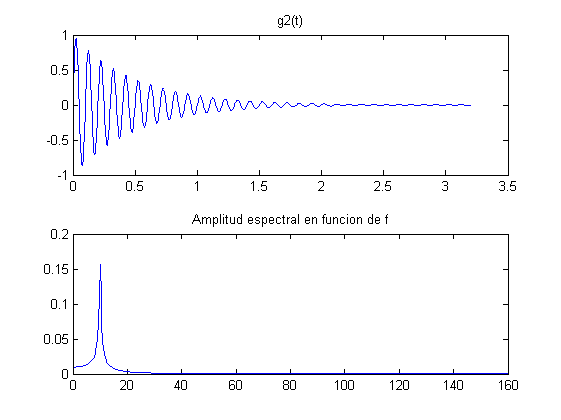
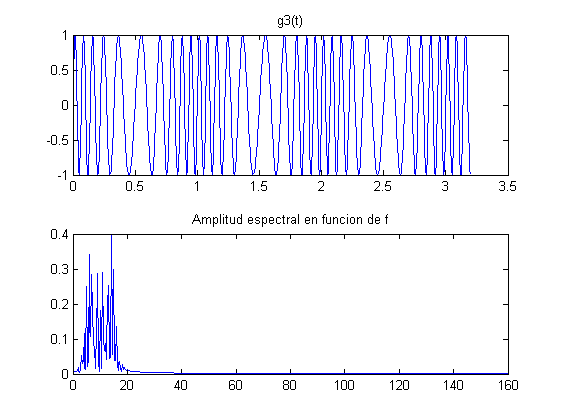
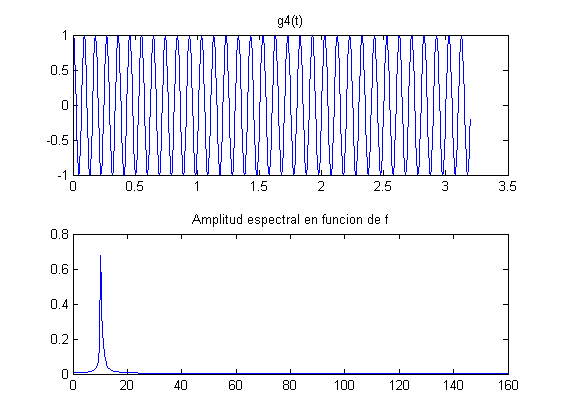
Tomando como base las condiciones del ejemplo de la transformada de Fourier de los apuntes (pág. 124), graficar para las siguientes señales la gráfica de la señal en el tiempo y la gráfica de la amplitud espectral en función de la frecuencia:

k = 5; m = 10; fo = 10; Bo = 2.5; N = 2^m; T = 2^k/fo;
ts = (0:N-1)*T/N;
df = (0:N/2-1)/T;

g1 = Bo*sin(2*pi*fo*ts)+Bo/2*sin(2*pi*fo*2*ts);
An1 = abs(fft(g1, N))/N;
figure(10)
subplot(2,1,1),plot(ts,g1),title('g1(t)')
subplot(2,1,2),plot(df, 2*An1(1:N/2)),title('Amplitud espectral en funcion de f')

g2 = sin(2*pi*fo*ts).*exp(-2*ts);
An2 = abs(fft(g2, N))/N;
figure(20)
subplot(2,1,1),plot(ts,g2),title('g2(t)')
subplot(2,1,2),plot(df, 2*An2(1:N/2)),title('Amplitud espectral en funcion de f')

g3 = sin(2*pi*fo*ts+5*sin((2*pi*fo/10)*ts));
An3 = abs(fft(g3, N))/N;
figure(30)
subplot(2,1,1),plot(ts,g3),title('g3(t)')
subplot(2,1,2),plot(df, 2*An3(1:N/2)),title('Amplitud espectral en funcion de f')

g4 = sin(2*pi*fo*ts-5*exp(-2*ts));
An4 = abs(fft(g4, N))/N;
figure(40)
subplot(2,1,1),plot(ts,g4),title('g4(t)')
subplot(2,1,2),plot(df, 2*An4(1:N/2)),title('Amplitud espectral en funcion de f')

Ejercicio 14

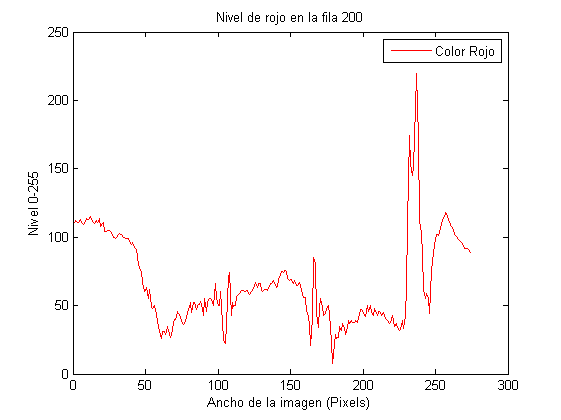
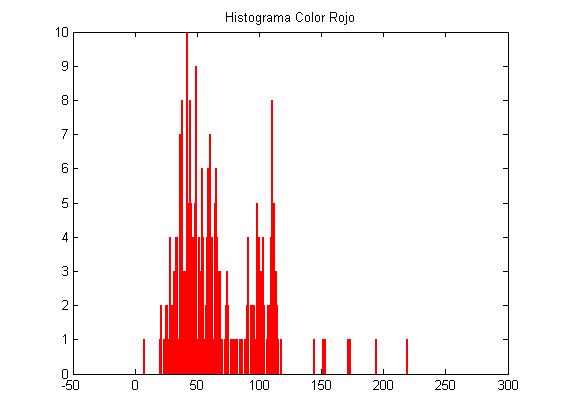
Leer y graficar la imagen WindTunnel.jpg de las transparencias y graficar en sendos gráficos el valor del color rojo de la imagen en función del ancho de la imagen y el histograma del mismo para una fila de la imagen que se pide al usuario. Mostrar el valor para 200

imagen=imread('WindTunnel.jpg');
close
figure(8);
imshow(imagen),title('WindTunnel.jpg')
[m, n, p]=size(imagen); %m filas, n columnas, p plano (r g b)
col=1:1:n; % ancho de la imagen
fil=200; % fila que queremos especificamente
%En caso de querer introducirlo por pantalla:
%fil = input('Fila de la imagen: ');
planoR=imagen(fil,col,1);
figure(2);
plot(col,planoR,'r'),ylabel('Nivel 0-255'),xlabel('Ancho de la imagen (Pixels)'),legend('Color Rojo'),title('Nivel de rojo en la fila 200')

for I = 1:256
    total(I)=0;
    for J = 1:n
     if planoR(J) == I;
        total(I)=total(I)+1;
     end
    end
end

figure(9)
valor=1:1:256;
bar(valor-1,total),title('Histograma Color Rojo')
rojo=[1 0 0];
colormap(rojo);

Published with MATLAB® R2014a